Introduction


When a beam of light hits the surface of an object, part of its energy is absorbed by the surface, part of its energy is reflected away and part of its energy may refract through the object itself.

In this post, we will explore the mathematics behind calculating the reflection vector.

Let:

  • \(L\) be the incoming light vector

  • \(N\) be the normal of the surface,

  • \(R\) be the reflection vector of \(L\),

  • \(\theta_i\) be the angle of incidence, and

  • \(\theta_r\) be the angle of reflection, and


    • We assume \(N\), \(L\) and \(R\) are normalized to unit length.



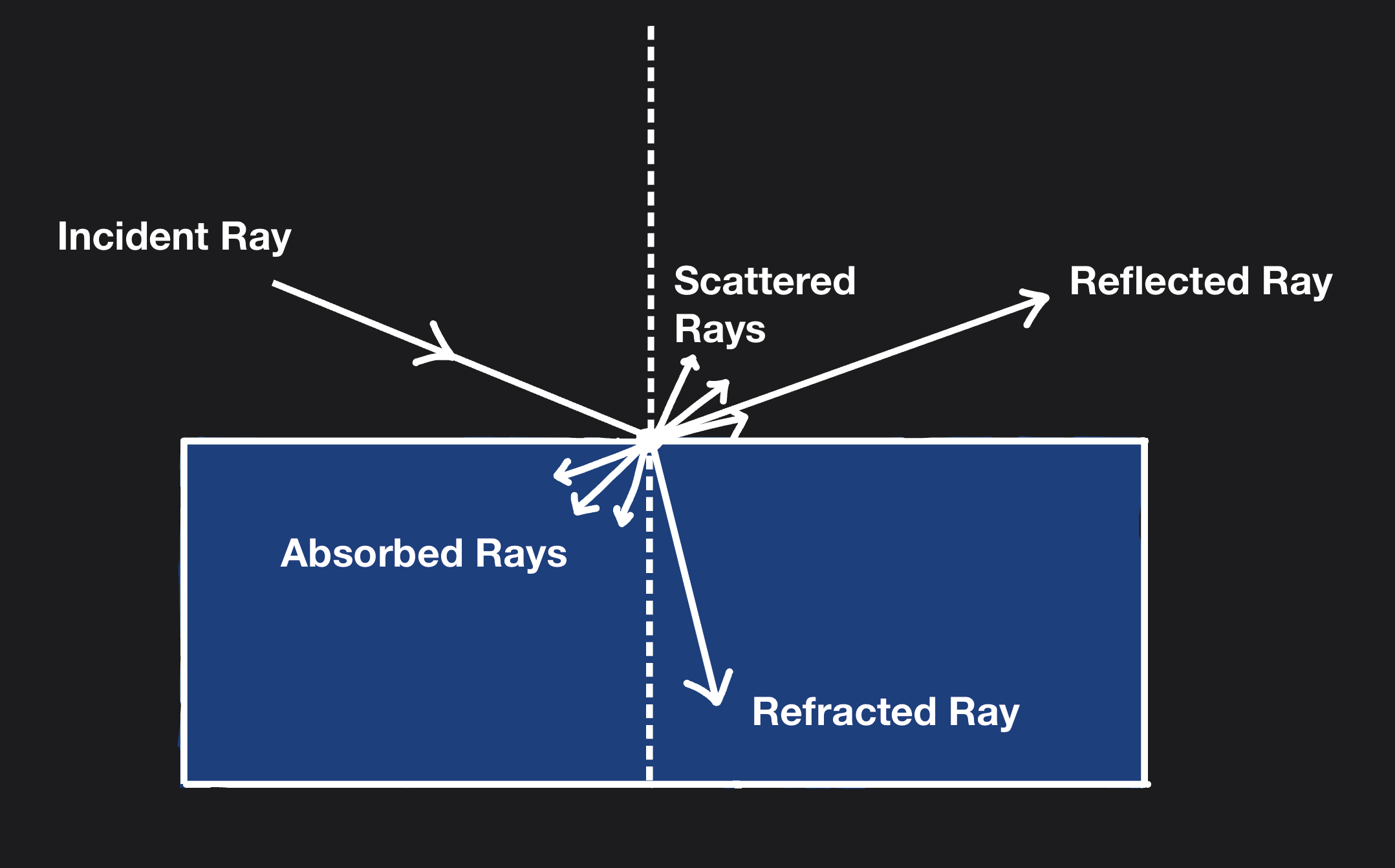
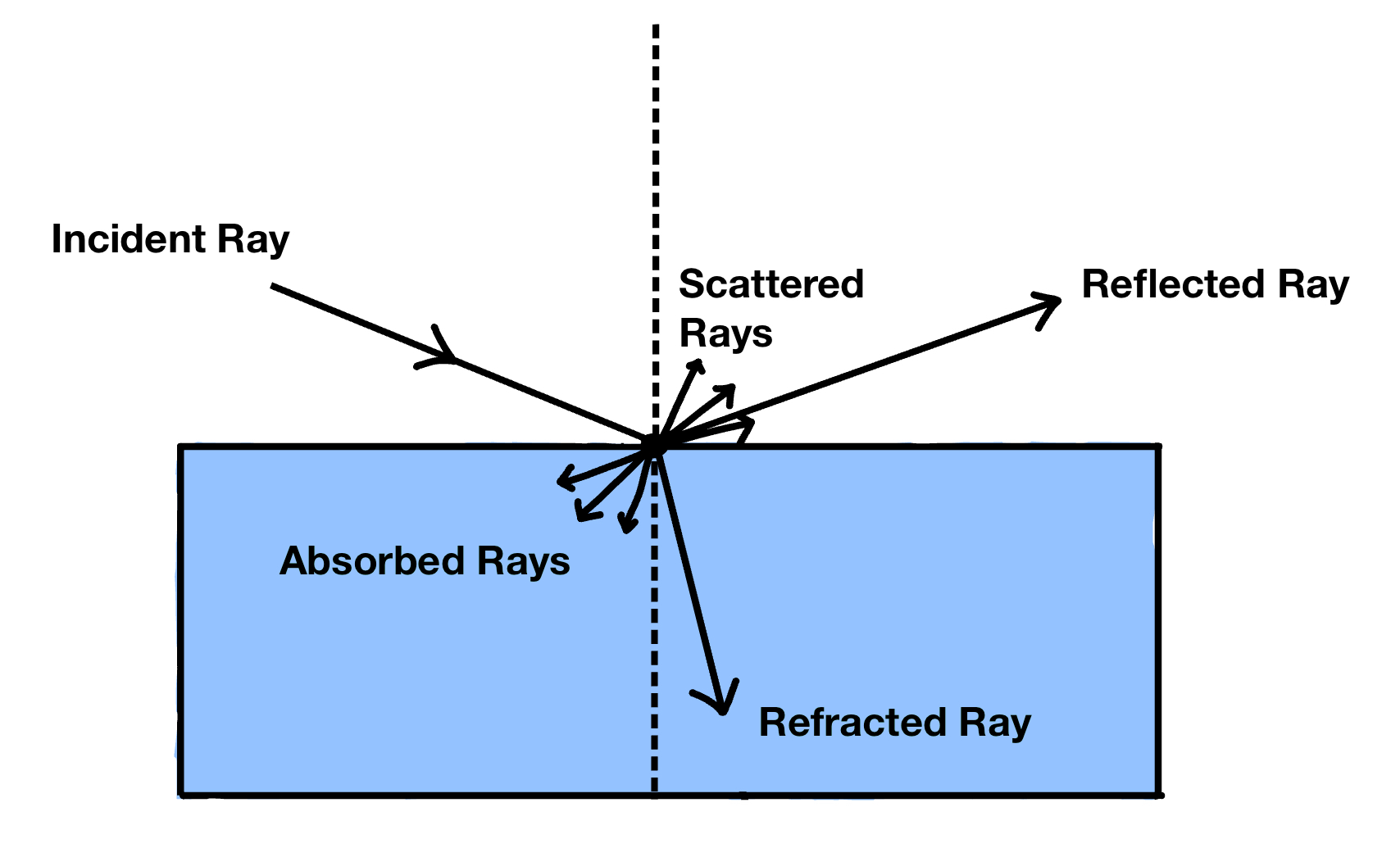
    Law of Reflection


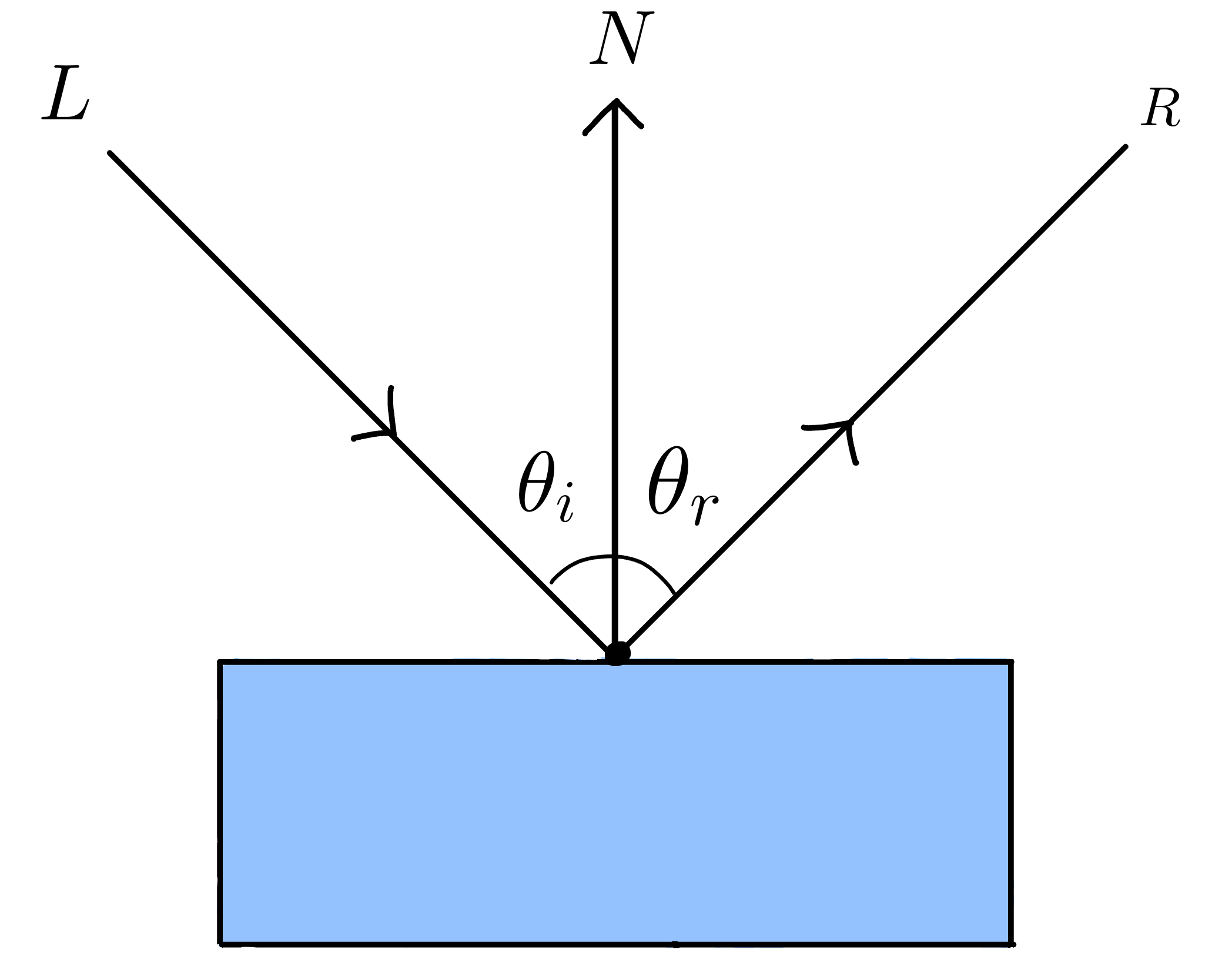
    The law of reflection states that the angle of incidence is equal to the angle of reflection. That is,

    \[\theta_i = \theta_r\]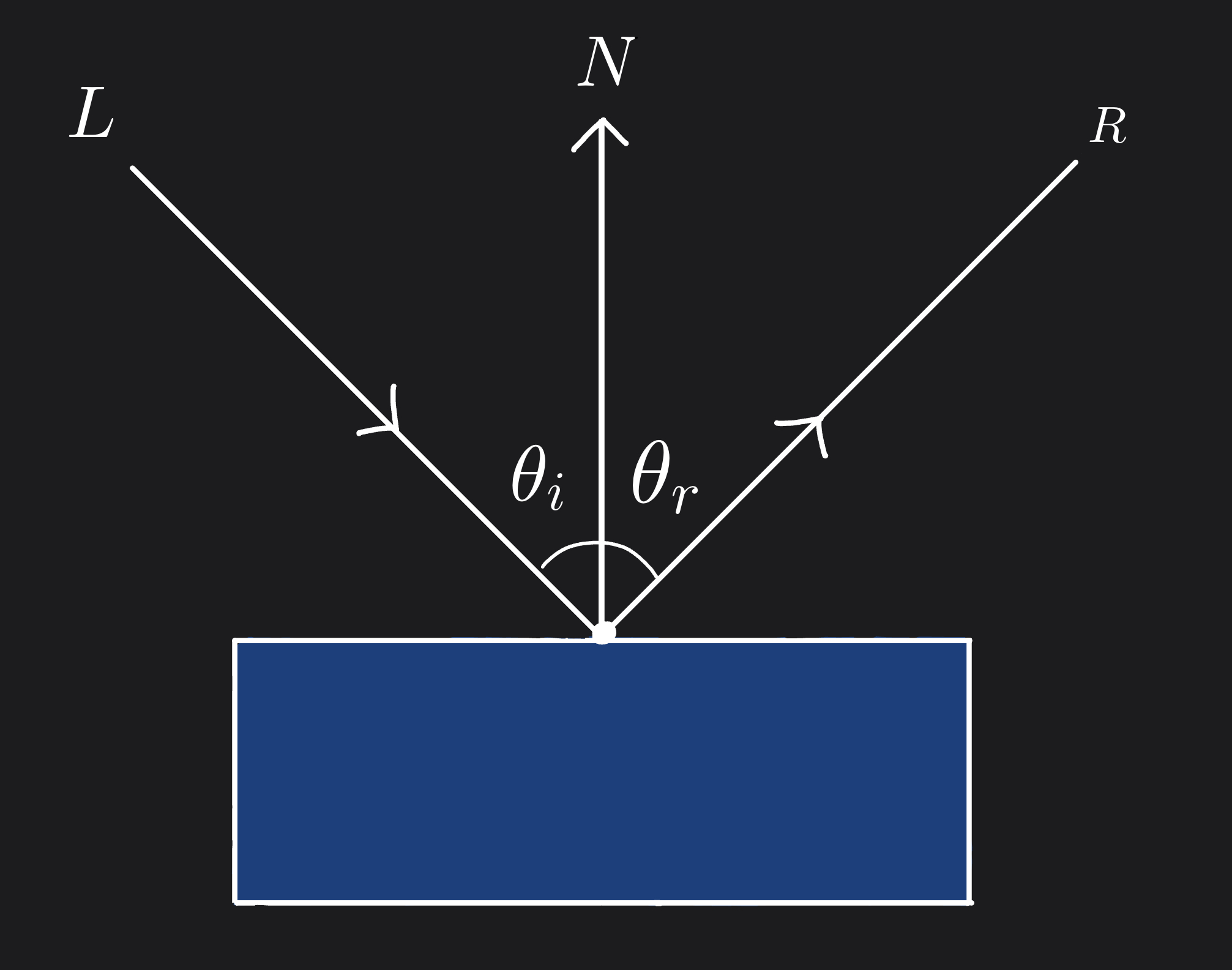




    Decomposition of Vector \(L\)


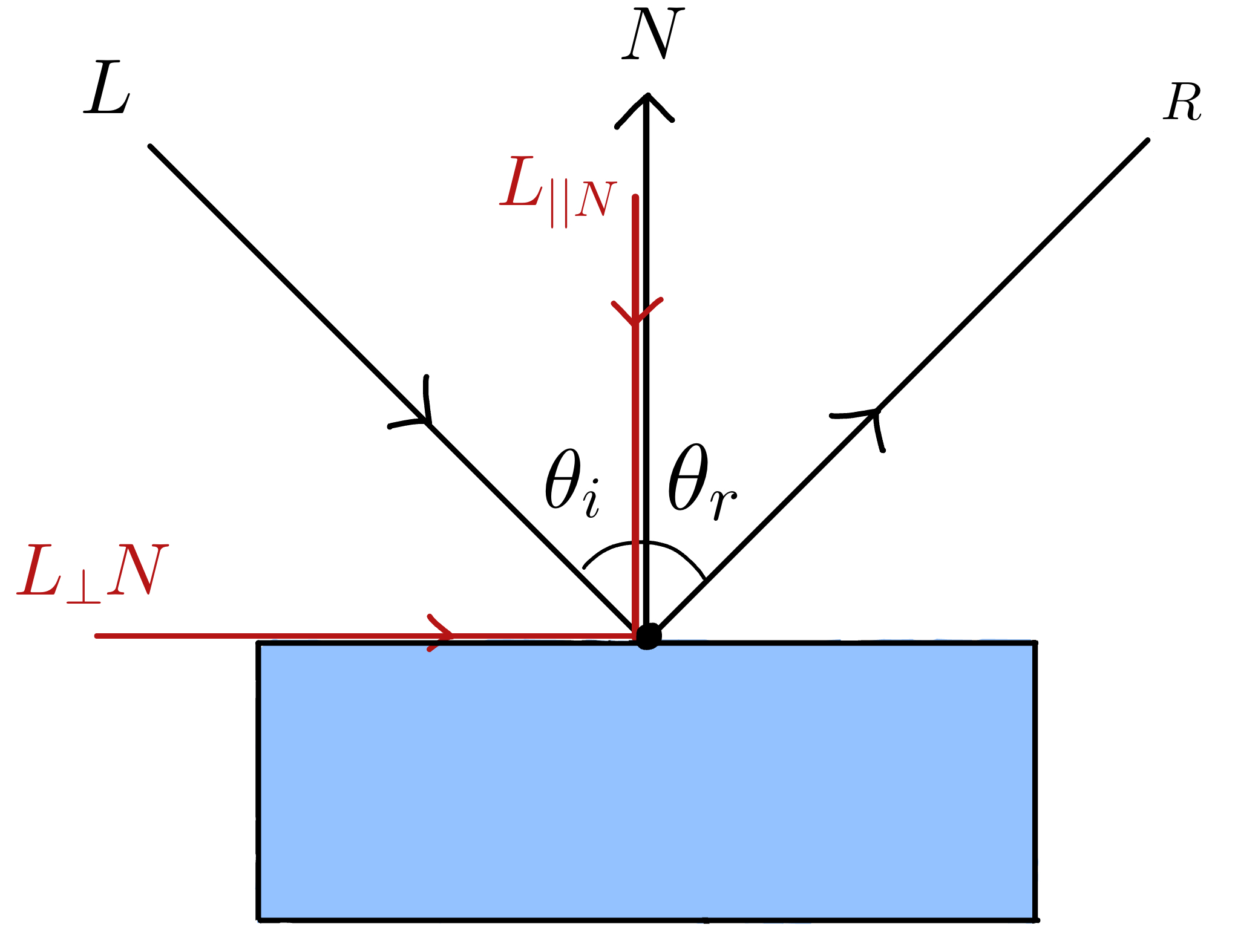
    To calculate the reflection vector \(R\), we first need to decompose the incoming light vector \(L\) in relation to the surface normal vector \(N\).

    The vector \(L\) has both a parallel component relative to \(N\) ; \(L_{||N}\) and a perpendicular component relative to \(N\) ; \(L_{⊥N}\) , such that

    \[L = L_{||N} + L_{⊥N}\]

    The parallel component of \(L\) along \(N\) is:

    \[L_{||N} = (L.N)N = N cos \theta\]

    The perpendicular component of \(L\) along \(N\) can be calculated by subtracting \(L_{||N}\) from \(L\) . That is,

    \[L_{⊥N} = L - L_{||N} = L - (L.N)N\]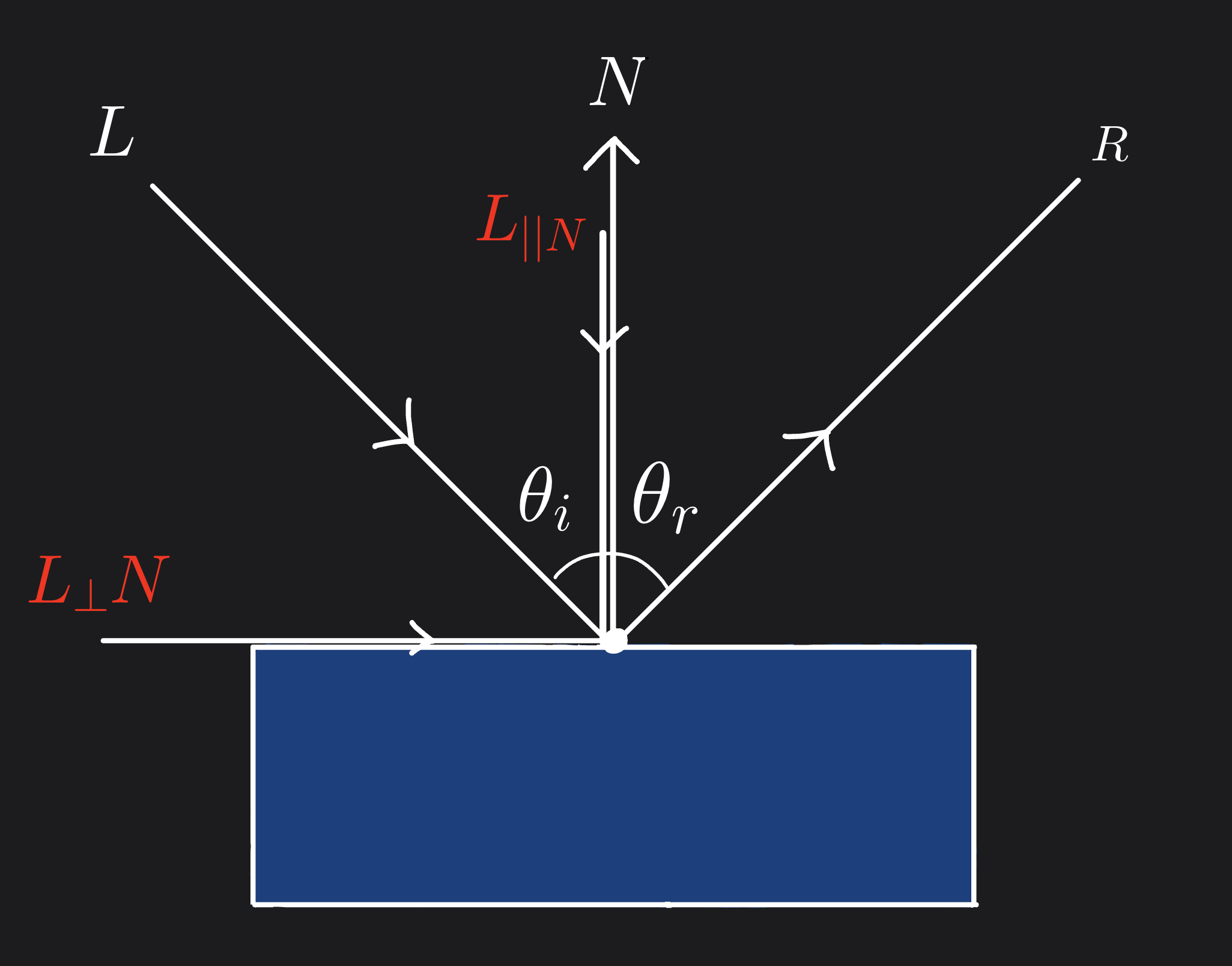



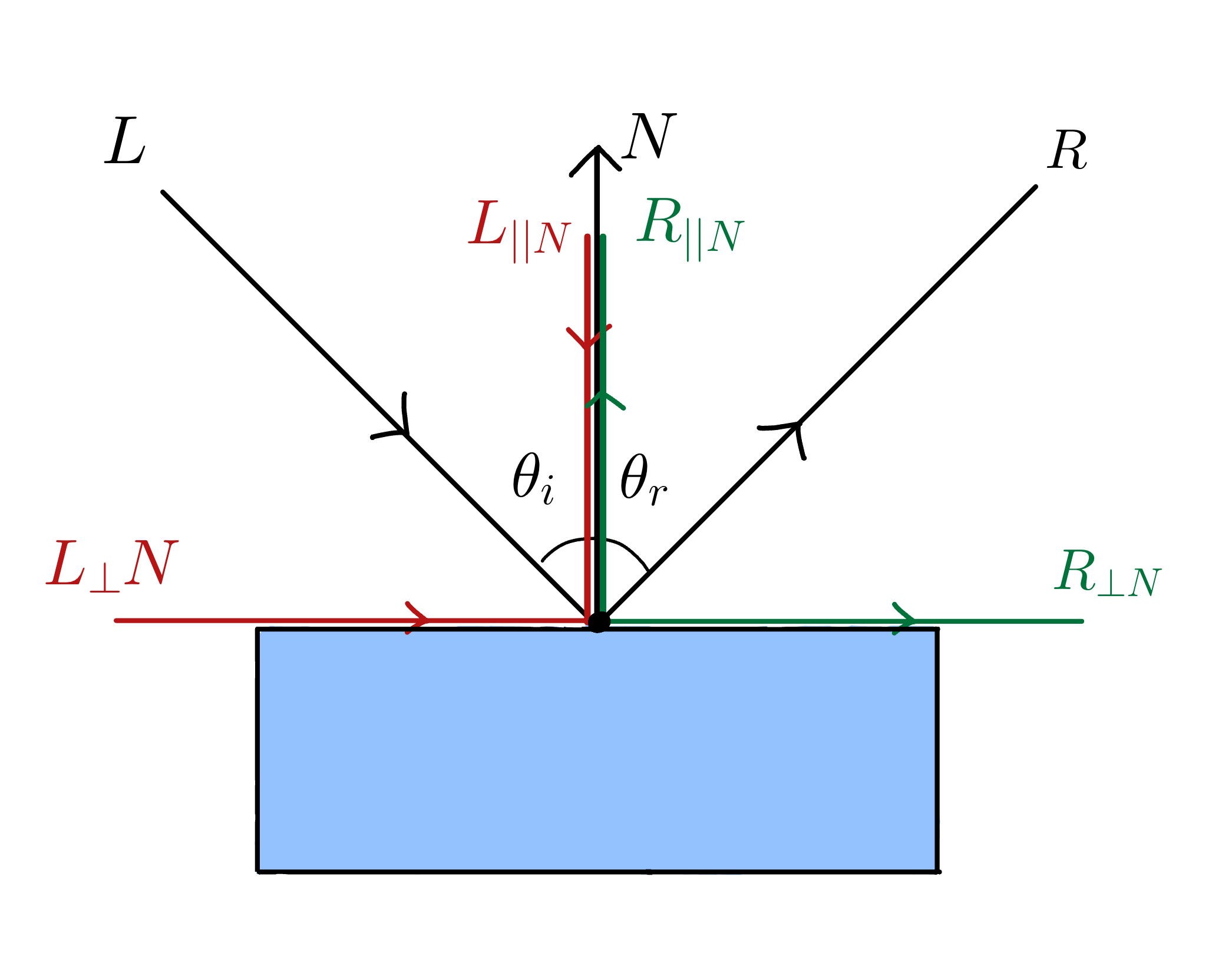
    Just like we did with the incoming light vector \(L\), we are going to decompose the reflection vector \(R\) in relation to the surface normal vector \(N\).

    The vector \(R\) has both a parallel component relative to \(N\) ; \(R_{||N}\) and a perpendicular component relative to \(N\) ; \(R_{⊥N}\) , such that

    \[R = R_{||N} + R_{⊥N}\]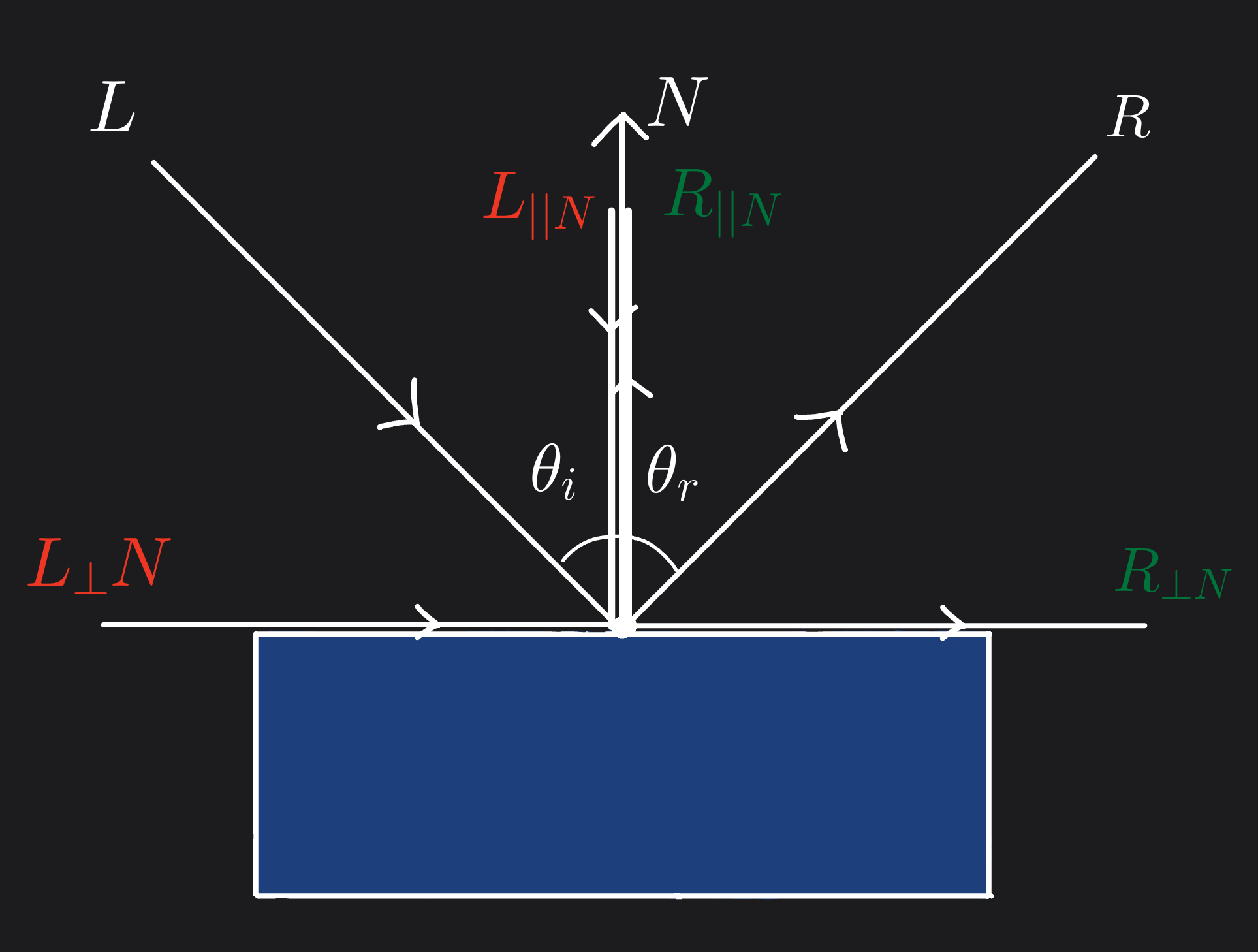




    Calculating the Reflection Vector \(R\)


    Now, let’s calculate the reflection vector \(R\). Since

    \[R = R_{||N} + R_{⊥N}\]

    then we can calculate \(R\) by calculating its components \(R_{||N}\) and \(R_{⊥N}\) .

    By the law of reflection, the angle of incidence is equal to the angle of reflection; i.e \(\theta_i = \theta_r\)

    This means that the components of \(R\) is equal in magnitude to the components of \(L\), but they may have opposite directions.

    The perpendicular component of \(R\) along \(N\) ; \(R_{⊥N}\) has the same direction as the perpendicular component of \(L\) along \(N\) ; \(L_{⊥N}\) .

    The parallel component of \(R\) along \(N\) ; \(R_{||N}\) , is in the opposite direction of the parallel component of \(L\) along \(N\) ; \(L_{||N}\) .

    Hence, the reflection vector \(R\) can be calculated as follows:

    \[R = L_⊥ - L_{||}\] \[R = L - (L.N)N - (L.N)N\] \[R = L - 2 (L.N)N\]


    Implementation


    The GLM library has a built-in function that computes the reflection vector, given the normal and incident vector. Here’s the C++ code using the GLM library:

    #include <glm/glm.hpp>
#include <glm/gtx/reflect.hpp>

glm::vec3 compute_reflection_vector( glm::vec3 L, glm::vec3 N )
{
    return glm::reflect(L, N) ;
}


    References


    • Chapter 6.4.1 - Mathematics for 3D Programming and Computer Graphics by Eric Lengyel