Introduction


When a beam of light hits the surface of an object, part of its energy is absorbed by the surface, part of its energy is reflected away and part of its energy may refract through the object itself.

In this post, we will explore the mathematics behind calculating the refraction vector.




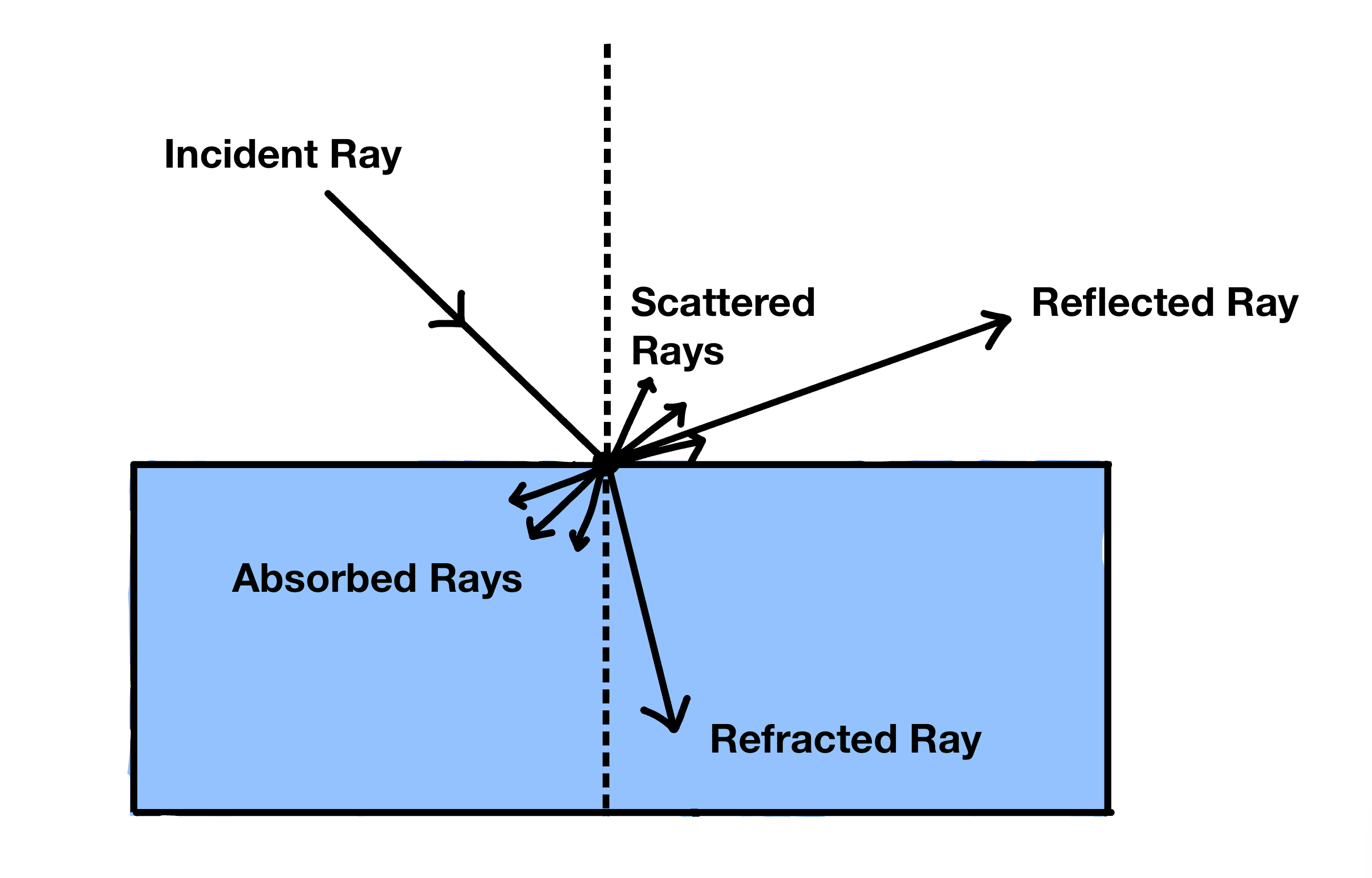
Snell Law


Transparent surfaces have a property called the index of refraction. This refractive index determines how much the path of light is bent or refracted, when entering a material. This can be explained by Snell’s Law.

Let:

  • \(n_L\) be the index of refraction of the material the light is leaving,
  • \(\theta_L\) be the angle of incidence,
  • \(n_T\) be the index of refraction of the material the light is entering, and
  • \(\theta_T\) be the angle of refraction.

According to Snell’s Law,

\[n_L sin \theta_L = n_T sin \theta_T\]

Each material has its own unique index of refraction. For example, the index of refraction of air is 1.000293, while the index of refraction of diamond is 2.417. Higher indexes of refraction create a greater bending effect at the interface between two materials, causing the refraction vector to bend more towards the normal vector.



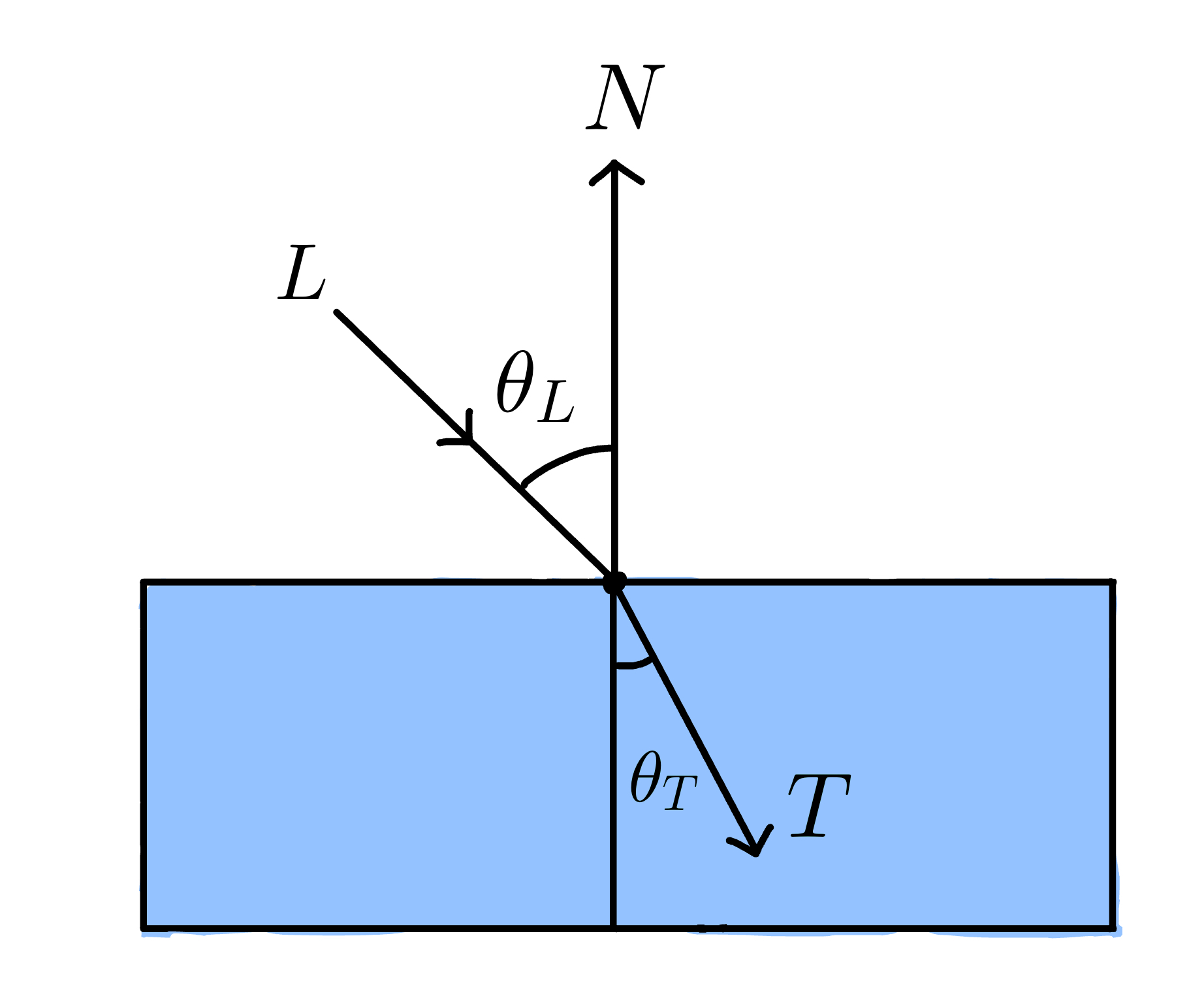
Now, let:

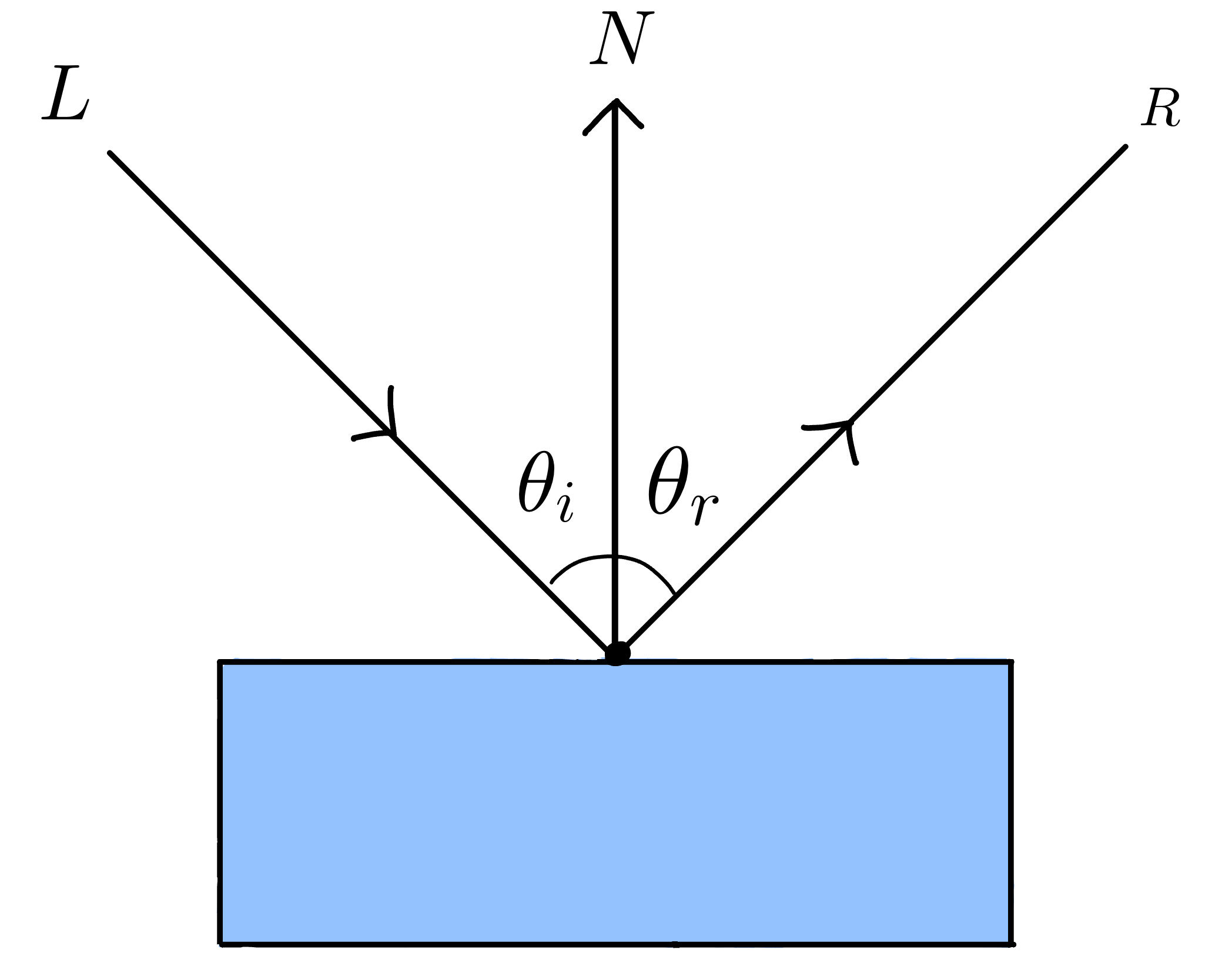
  • \(L\) be the incoming light vector,
  • \(N\) be the normal vector, and
  • \(T\) be the refracted light vector.

We assume that \(L\), \(N\) and \(T\) are normalized to unit length.


Decomposition of Incoming Light Vector \(L\)


To calculate the refraction vector \(T\), we first need to decompose the incoming light vector \(L\) in relation to the surface normal vector \(N\).

Each vector has both a parallel component and perpendicular component relative to the normal vector \(N\).



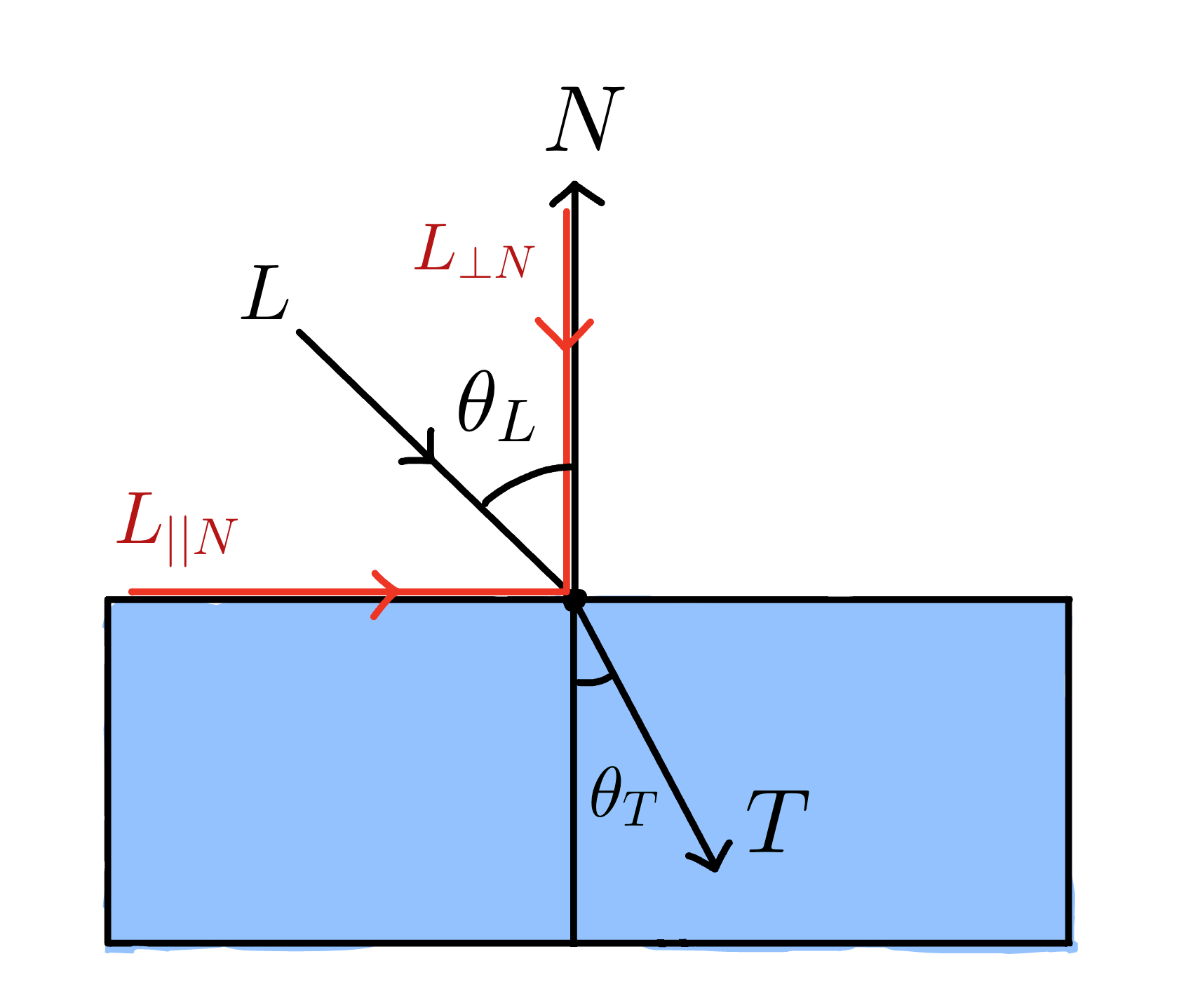
The parallel component of \(L\) along \(N\) is

\[L_{||N} = (N.L)N = N cos \theta_L\]

The perpendicular component of \(L\) along \(N\) can be calculated by subtracting \(L_{||N}\) from \(L\) . That is,

\[L_{⊥N} = L - L_{||N} = L - (N.L)N\]

Next, let’s calculate the magnitudes of \(L_{||N}\) and \(L_{⊥N}\)

Since the vectors \(L\) , \(L_{||N}\) and \(L_{⊥N}\) form a right-angled triangle, we can use trignometric relationships to calculate their magnitudes.

We know that

\[sin\theta_L = \frac{|L_{⊥N}|}{L}\]

and

\[cos\theta_L = \frac{|L_{||N}|}{L}\]

Since \(L\) has been normalized to unit length (i.e., \(|L| = 1\) ), then

\[|L_{⊥N}| = sin \theta_L\]

and

\[|L_{||N}| = cos \theta_L\]


Decomposition of Refraction Vector \(T\)


Just like we did with the incoming light vector \(L\), we are going to decompose the refraction vector \(T\) in relation to the surface normal vector \(N\).



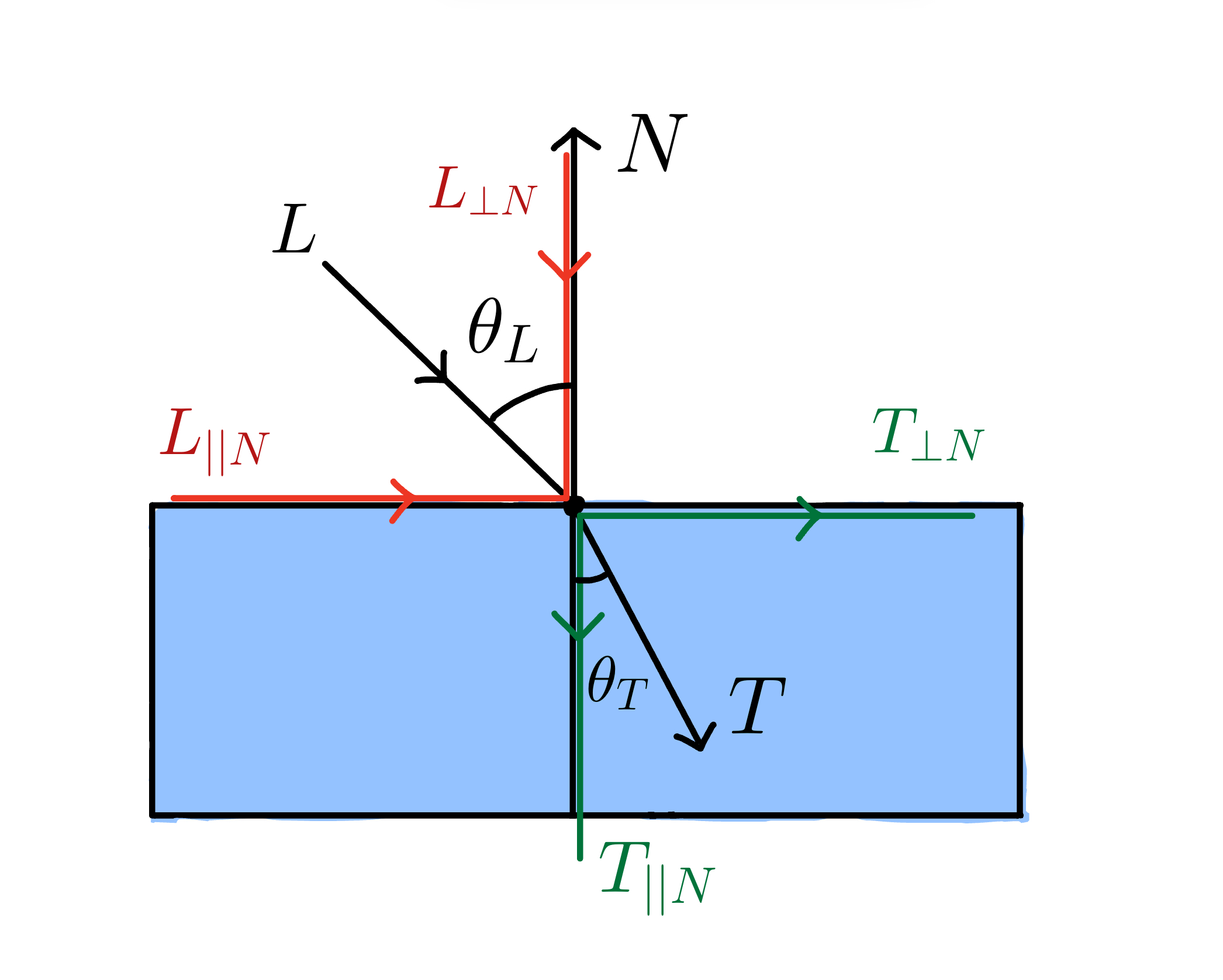
The parallel component of \(T\) along \(N\) is

\[T_{||N} = (-N.T)(-N) = -N cos \theta_T\]

As we know, we can calculate the perpendicular component of \(T\) along \(N\) as:

\[T_{⊥N} = T - T_{||}\]

However, we do not know \(T\). Hence, we must find another way to calculate \(T_{⊥N}\).

Let’s first calculate the magnitudes of \(T_{||N}\) and \(T_{⊥N}\) .

Since the vectors \(T\) , \(T_{||N}\) and \(T_{⊥N}\) form a right-angled triangle, we can use trignometric relationships to calculate their magnitudes.

We know that

\[sin\theta_T = \frac{|T_{⊥N}|}{|T|}\]

and

\[cos\theta_T = \frac{|T_{||}|}{T}\]

Since \(T\) is normalized to unit length(i.e., \(|T| = 1\) . Then,

\[|T_{⊥N}| = sin\theta_T\]

Now that we have \(|T_{⊥N}|\) , let’s return to the problem of calculating \(T_{⊥N}\) .

Since \(T_{⊥N}\) has the same direction as \(L_{⊥N}\), then we can calculate \(T_⊥\) as:

\[T_⊥ = \frac{L_{⊥N}}{|L_{⊥N}|} |T_{⊥N}| = \frac{L_{⊥N}}{|L_{⊥N}|} sin \theta_T = \frac{L-(N.L)N}{sin \theta_L} sin \theta_T\]


Calculation of Refraction Vector \(T\)


Finally, we can calculate the refraction vector \(T\) by adding \(T_{||N}\) and \(T_{⊥N}\) . That is,

\[T = T_{||N} + T_{⊥N}\] \[T = (-N.T)(-N) + \frac{L-(N.L)N}{sin \theta_L} sin \theta_T\] \[T = -N cos \theta_T + \frac{L-(N.L)N}{sin \theta_L} sin \theta_T\]

Let’s do some further simplification to the equation.

We can use Snell Law to replace \(\frac{sin\theta_T}{sin\theta_L}\) with \(\frac{n_L}{n_T}\). This yields:

\[T = -N cos \theta_T + \frac{n_L}{n_T}(L-(N.L)N)\]

We can also replace \(cos \theta_T\) with \(\sqrt{1-sin^2 \theta_T}\) , which gives us

\[T = -N \sqrt{1-sin^2 \theta_T} + \frac{n_L}{n_T}(L-(N.L)N)\]

Furthermore, we can use Snell Law to replace \(sin^2 \theta_T\) with \(\frac{n_L^2}{n_T^2} sin^2 \theta_L\) . The result is

\[T = -N \sqrt{1-\frac{n_L^2}{n_T^2} sin^2 \theta_L} + \frac{n_L}{n_T}(L-(N.L)N)\]

Finally, we can replace \(sin^2 \theta_L\) with \(1-cos^2 \theta_L = 1 - (N.L)^2\)

This gives us:

\[T = -N \sqrt{1-\frac{n_L^2}{n_T^2} (1-(N.L)^2)} + \frac{n_L}{n_T}(L-(N.L)N)\] \[T = -N \sqrt{1-\frac{n_L^2}{n_T^2} (1-(N.L)^2)} + \frac{n_L}{n_T}L - \frac{n_L}{n_T}(N.L)N\]

\begin{equation} T = N ( - \frac{n_L}{n_T}(N.L) - \sqrt{1-\frac{n_L^2}{n_T^2} (1-(N.L)^2)} ) + \frac{n_L}{n_T}L \end{equation}

Now, if you noticed, equation 1 contains a radical. If the quantity inside the radical is negative, the equation becomes invalid.

To be more specific, equation 1 can become invalid if \(n_L > n_T\) . This phenomena is called Total Internal Reflection, which means that no refraction is happening and the vector is reflecting off the surface. In this case, the equation for calculating the reflection vector is the one used.



Expressed another way, we can say that equation 1 is only valid when

\[sin \theta_L \leq \frac{n_T}{n_L}\]

Why ?

Well, let’s prove it.


Proof


From equation 1, we can deduce that the equation becomes invalid when the quantity inside the radical becomes negative.

Hence, equation 1 is valid only when

\[1-\frac{n_L^2}{n_T^2} (1-(N.L)^2) \geq 0\]

Rearranging the equation gives us:

\[\frac{n_L^2}{n_T^2} (1-(N.L)^2) \leq 1\]

We can divide both sides by \(\frac{n_L^2}{n_T^2}\) . This yields:

\[1-(N.L)^2 \leq \frac{n_T^2}{n_L^2}\]

Multiplying by -1 gives us:

\[(N.L)^2 -1 \geq - \frac{n_T^2}{n_L^2}\] \[(N.L)^2 \geq 1 - \frac{n_T^2}{n_L^2}\]

Now, since \(N.L = cos \theta_L\) , then

\[cos^2 \theta_L \geq 1 - \frac{n_T^2}{n_L^2}\]

We know that \(cos^2 \theta_L = 1 - sin^2 \theta_L\) . Hence,

\[1 - sin^2 \theta_L \geq 1 - \frac{n_T^2}{n_L^2}\]

Finally, rearranging the equation, multiplying by -1 and taking the square root in both sides gives us:

\[sin^2 \theta_L \leq \frac{n_T^2}{n_L^2}\] \[sin \theta_L \leq \frac{n_T}{n_L}\]

This completes the proof that equation 1 is only valid when

\[sin \theta_L \leq \frac{n_T}{n_L}\]


References


  • Chapter 6.4.2 - Mathematics for 3D Programming and Computer Graphics by Eric Lengyel




Need help with computer graphics?

I offer one-on-one tutoring for students and professionals, covering all levels of computer graphics along with the APIs OpenGL, WebGL, Vulkan, Metal, and Direct3D for developing game engines, simulations, animations, and video games.

Learn more → Tutoring